Описательная статистика (Descriptive statistics)
Descriptive statistics are a collection of measurements of two things: location and variability. Location tells you the central value of your variable (the mean is the most common measure). Variability refers to the spread of the data from the center value (i.e. variance, standard deviation).
Statistics is basically the study of what causes variability in the data. Популяция (или генеральная совокупность) – это вся группа объектов, которая нас интересует. Выборка (или выборочная совокупность) – это подмножество (часть) популяции. Основной вопрос статистики – это как на основании выборки сделать выводы обо всей популяции? Если наша выборка состоит из n наблюдений X1, ..., Xn, то выборочное среднее (или «среднее по выборке») равно $\overline{X} = \frac{\sum_{i=1}^{n} X_i}{n}$. Поскольку все наблюдения X1, …, Xn имеют математическое ожидание $\mu$, среднее этих наблюдений (т.е., выборочное среднее) тоже имеет математическое ожидание $\mu$: $E\left( \overline{X} \right) =$ $\left( \frac{\sum_{i=1}^{n} X_i}{n} \right) =$ $\frac{\sum_{i=1}^{n} E\left( X_i \right)}{n} =$ $E\left( X_i \right) =$ $\mu$.
Краткое введение в Описательную статистику в прилагаемом pdf на русском языке, а также на английском от Принстонского университета.
Понятие Constructs и еще ссылка. С разбора этого понятия начинаются многие курсы по анализу данных.
Основные меры центральной тенденции - число, служащее для описания множества значений одним-единственным числом.
Основные понятия описательной статистики на Wolfram MathWorld.
Математическое ожидание (а также среднее, mean, expected value, EV, M(X), $\mu_x$) случайной величины X с функцией вероятности P(X = x) есть $E (X) = \sum {x*P(X = x)}$, где суммирование ведется по всем возможным х. Поскольку P(X = x) это вероятность, она всегда находится между 0 и 1: 0 ≤ P(X = x) ≤ 1 для любого х. Кроме того, если мы просуммируем P(X = x) для всех возможных значений x, мы получим 1. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: $E(X) =$ $M(X) = \sum \limits_{n=1}^{\infty}x_i p_i$. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина! Вероятностный смысл: Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины: $\overline{X} \simeq E(X)$. Происхождение термина "математическое ожидание" связано с начальным периодом возникновения теории вероятностей (XVI-XVII вв.), когда область ее применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша, или, иными словами, математическое ожидание выигрыша. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [a, b], называют определенный интеграл $M(X) =$ $E(X) = \int\limits_a^b xf(x)\,dx$. А если возможные значения принадлежат всей оси Ox, то $M(X) =$ $E(X) = \int\limits_{-\infty}^{\infty} xf(x)\,dx$. Здесь можно найти очень наглядное визуальное представление понятия "математическое ожидание" на примере игральной кости.
Стандартная ошибка среднего в математической статистике на Wiki.
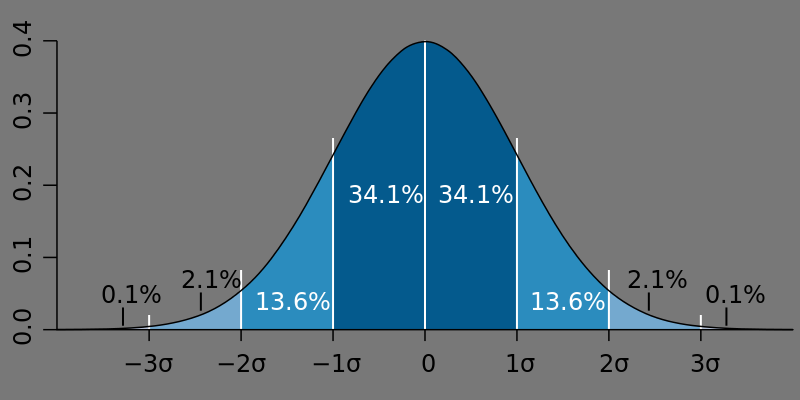
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью $f(x) =\frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$, где $\mu$ есть математическое ожидание, а $\sigma$ - среднее квадратическое отклонение нормального распределения. При вычислении вероятностей, связанных с нормальным распределением, мы используем стандартизацию: если $Х\sim(\mu, \sigma^2)$, то $(Х-\mu)/\sigma \sim N(0, 1)$ – то есть, преобразованная случайная величина $Z=(Х-\mu)/\sigma$ имеет «стандартное нормальное распределение» - со средним 0 и стандартным отклонением 1. Случайная величина Z называется «стандартной нормальной величиной». Значение Z ( Z-score, Z-оценка) говорит нам о числе стандартных отклонений, в которых X лежит от своего среднего. Standard normal table. Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием $\mu = 0$ и стандартным отклонением $\sigma = 1$. Функция плотности стандартного нормального распределения: $f(x) =\frac{1}{\sqrt{2\pi}} e^{-\frac{z^2}{2}}$.
Центральная предельная теорема (ЦПТ): сумма большого числа как угодно распределенных независимых случайных величин распределена асимптотически нормально, если только слагаемые вносят равномерно малый вклад в сумму. Пусть X1, ..., Xn, ... - бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание $\mu$ и дисперсию $\sigma^2$. Пусть $S_n = \sum \limits_{i=1}^{n} X_i$ и $N(0,1)$ - нормальное распределение с параметрами $\mu=0$, $\sigma^2=1$. Тогда $\frac{S_n-\mu n}{\sigma \sqrt{n}} \rightarrow N(0,1)$ по распределению при $n \to \infty$. Обозначив символом $\overline{X}$ выборочное среднее первых n величин, то есть $\overline{X}=\frac{1}{n} \sum \limits_{i=1}^{n} X_i $, мы можем переписать результат центральной предельной теоремы в следующем виде: $\frac{\overline{X}-\mu}{\sigma \sqrt{n}} \rightarrow N(0,1)$ по распределению при $n \to \infty$. Central limit theorem на Wiki, а также в блоге Rajesh Singh. Доказательства теоремы от CS at U of T и еще одно от UC Berkeley.
Упрощенное определение ЦПТ: если размер случайной выборки n достаточно велик, то нам не важно, какой формы распределение в популяции. Независимо от этого, выборочное среднее будет распределено по нормальному закону! Для практических целей, размер выборки n≥30 достаточен для того, чтобы выборочное среднее было распределено нормально. Рассмотрим случайную выборку размера n≥30 из любой популяции (т.е., распределения любой формы) со средним $\mu$ и стандартным отклонением $\sigma$. Тогда выборочное среднее $\overline{X}$ распределено по нормальному закону со средним $\mu$ и стандартным отклонением $\frac{\sigma}{\sqrt{n}}$: $\overline{X}\sim N\left(\mu, \frac{\sigma^2}{n}\right)$.